"A meggyőző lehetetlen mindig jobb, mint a nem meggyőző lehetséges." (Arisztotelész)

Escher mestere volt a lehetetlen meggyőző ábrázolásának, s bár nem ő volt az első, aki lehetetlen valóságot ábrázolt, ő volt az, aki igazán népszerűsítette, és a köztudatba hozta ezeket az alakzatokat. Mielőtt azonban röviden áttekintenénk az Escher lehetetlen képeit megelőző, s azokat inspiráló korábbi paradox képeket, szükséges meghatározni a lehetetlen tárgy definícióját. "A lehetetlen tárgy olyan kétdimenziós ábrázolás, amely háromdimenziós tárgy vagy helyzet reprezentációjának tűnik, de a térbeli információk ellentmondásosak, vagy a kép elemei olyan kombinációban szerepelnek, ahogy tapasztalatunk szerint nem fordulhatnak elő a valóságban". Azt is mondhatjuk, hogy ha ábrázoláskor a tér logikáját figyelmen kívül hagyjuk, lehetetlen alakzathoz jutunk. Ilyen ábrákra és képekre számtalan példa van a művészetben, sőt mint látni fogjuk matematikus is foglalkozott velük. A következőkben néhány, a teljesség igénye nélkül kiragadott példa szerepel.

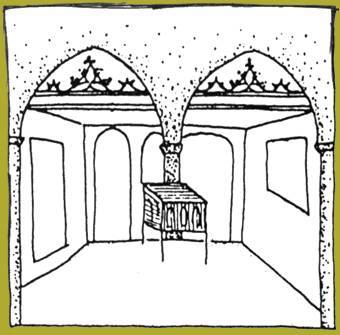
Bruno Ernst vázlata az Angyali üdvözlet c. freskóról

Az egyik legkorábbi mű a holland, bredai Grote Kerk 1902-ben, egy restaurálás során felfedezett freskója. Az ismeretlen XV. századi festő a három, képen szereplő oszlop közül a középsőt lehetetlen módon ábrázolta: míg a két szélső az előtérben helyezkedik el, addig a középső a háttérben. A művész célja ezzel az elrendezéssel nem a meghökkentés vol, hanem csak egyszerűen nem akarta a kompozíció egységét megtörni egy oszloppal az előtérben.

A modern belga művész, Jos de Mey számos alkalommal használta ezt a típusú lehetetlen alakzatot munkáiban. Egyik ilyen képe:

Itt is a kép sztereografikus elemei vannak ellentmondásban egymással, vagyis a térbeli elrendezés az, ami paradox.

Ennél összetettebb képet készített Giovanni Battista Piranesi, olasz rézmetsző, Carceri (börtönök) címmel.

Olyan teret próbált megalkotni, ami teljesen összezavarja a szemlélőt. Noha a mű erősen háromdimenzió benyomását kelti, tele van dimenziós ellentmondásokkal. Azt mondhatnánk Piranesi lehetetlen teret próbált ábrázolni. Ezért nem meglepő, hogy lehetetlen alakzatokat alkalmazott erre a célra. A B-vel jelzett oszlop az előtérből indul, és ott is végződik.

Hogy méginkább hangsúlyozza a kép lehetetlen voltát Piranesi még elhelyezett egy, a fallal párhuzamos lépcsőt is, ami a fal mögé nyúlik, s ez szintén lehetetlen. A jobb oldali ábrán vázlatosan látszik mi is történik a képen.

Ezekből a művekből jól látszik, hogy lehetetlen alakzattal már korábban is foglalkozott a nyugati művészet, de igazán markánsan csak Oscar Reutersvärd munkáiban jelent meg 1934-től. Még középiskolás diák, amikor véletlenül rajzolt egy paradox ábrát. S noha matematikai enciklopédiákban nem talált semmiféle utalást erre a különleges geometriai alakzatra, a következő években folytatta a tér logikájának ellentmondó ábrák készítését. Eljátszott a paradox kombinációkban álló kockákkal, megalkotta a végtelen lépcsőt és az ördögvillát, ami kicsit különbözött a ma ismert alaktól.

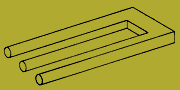
Az ördögvilla mai változata


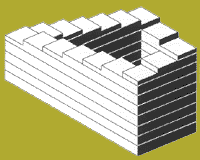
Reutersvärd: Végtelen lépcső

1958-ban vált tudatossá benne , hogy amiket kisfiúként rajzolt, valójában lehetetlen tárgyak. Ekkor szerzett ugyanis tudomást egy cikkből arról, hogy tőle függetlenül Lionel Penrose is felfedezte a végtelen lépcsőt. Elmélyedt hát a paradox alakzatok témájában, s azóta több mint 2500 lehetetlen ábrát rajzolt. Ezek közül néhány itt látható:

Reutersvärd:

Lehetetlen háromszög Lehetetlen háromszögek kombinációja Lehetetlen alakzat

A lehetetlen háromszögről később még részletesen szólunk.

Reutersvärd: Meanderszerű alakzat

Reutersvärd meanderszerű formájának két párhuzamos hasábot látunk, de a vonalas rajzként létezhet; térbeli lehetetlenségére egyszerűen az alakzat kiszínezésével is rávilágíthatunk.

Kulpa: Lehetetlen hasábok

Zenon Kulpa rajzán első ránézésre kontúrjai kétértelműek. Az ábra csak jobb oldali a másik árnyékává válik, s ezáltal eltűnik a szemünk elől.

Ilyen és ehhez hasonló képek voltak Escher lehetetlen ábráinak az előfutárai, melyekből a holland grafikus ötletet meríthetett, de gazdag fantáziavilágának köszönhetően újat is tudott nyújtani. Oly annyira újat és különlegeset alkotott, hogy a nagyközönség is leginkább az ő nevével fémjelzett litográfiákhoz köti a lehetetlen tárgy fogalmát; s egyáltalán, ezek a művek azok, melyek a lehetetlen alakzatokat széles körben ismertté és népszerűvé tették.

Noha Escher lehetetlen valóságot ábrázoló képeit nem lehet szigorú kategóriákba sorolni, három fő trend azért mégis észrevehető.